1.1.1 Types of numbers
1.1.1 Types of numbers
1.1.1 Numbers
We use numbers in our day-to-day life.
They are often called numerals.
Without numbers, we cannot do counting of things, date, time, money, etc. Sometimes these numbers are used for measurement and sometimes they are used for labelling.
The properties of numbers make them capable of performing arithmetic operations on them.
These numbers are expressed in numeric forms and also in words. For example, \( 2 \) is written as two in words, \( 25 \) is written as twenty-five in words, etc. There are different types of numbers in Math, which we learn here.
1.1.2 Types of numbers
Natural numbers:
The numbers which are used to count are called natural numbers.
\( 1 \) , \( 2 \) ,\( 3 \), \( 4 \). . . are natural numbers.
For natural numbers, the letter \( N \) is frequently used.
Whole numbers:
Natural numbers including ‘\( 0 \)’ are known as whole numbers.
For whole numbers, the letter \( W \) is frequently used.
Integers:
Integers are whole numbers. They can be positive or negative.
\( 0 \) ,\( \pm 1 \) , \( \pm 2 \) , \( \pm 3 \) , \( \pm 4 \) . . . are integers.
For integers, the letter \( Z \) is frequently used.
Positive Integers:
\( +1 \) , \( +2 \) , \( +3 \) , \( +4 \) . . . are positive integers.
Negative Integers:
\( -1 \) , \( -2 \) , \( -3 \) , \( -4 \) . . . are negative integers.
Neither positive nor negative:
‘\( 0 \)’ is the only integer which is neither positive nor negative.
Reciprocals:
A number’s reciprocal is obtained by dividing it by one.
- Any integer will equal one when multiplied by its reciprocal.
- The reciprocal of \( 3 \) is \( \frac{1}{3} \) and reciprocal of \( \frac{1}{3} \) is \( 3 \)
- Reciprocal of -\( \frac{1}{3} \)of is \( -3 \).
- The reciprocal of a number \( n \) can also be expressed as \( n^{-1} \)
Rational numbers:
A number which can be expressed as a ratio of two integers, where denominator should not be
zero, known as a rational number.
e.g.
- \( 0.3 \) recur \( =0.3333 . . .= \frac{1}{3} \) is a rational number.
- \( 0.25= \frac{25}{100} = \frac{1}{4} \) is a rational number.
Irrational numbers:
A number which cannot be expressed as a fraction of two integers known as an irrational number.
e.g.
- \( \pi \), \( \sqrt{2} \), \( \sqrt{3} \) , \( \sqrt{5} \) are irrational numbers.
- The number \( \sqrt{n} \) is an irrational number if n is not a square number
- Any multiple of an irrational number is also irrational
Exam tip
- You might be asked to pick an irrational number from a list.
- If you’re uncertain if a number is rational or irrational, input it into your calculator to determine if a fraction may be displayed.
- Where feasible, calculators may display irrational numbers in their actual form rather than as a decimal.
- The calculator will show the number rounded to \( 9 \) or \( 10 \) decimal places if it can’t display the exact form.
Worked Example:
Explain why \( \sqrt{7} \) is an irrational number?
Because it cannot be expressed as a fraction.
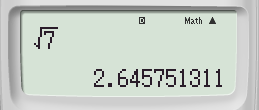
Real numbers:
Real numbers are the numbers which include both rational and irrational numbers.
For real numbers, the letter \( R \) is frequently used.
e.g.
\( 2 \), \( -3 \), \( \sqrt{ \frac{2}{5} } \), \( \sqrt{37} \), \( \frac{4}{5} \), are real numbers.
Multiples:
The outcomes of the times tables are the multiples of a given number.
There is an infinite list of multiples of every non-zero number.
e.g.
- Multiples of \( 2 \) are \( 2,4,6,8,10,12. . . \)
- Multiples of \( 6 \) are \( 6,12,18,24,30. . . \)
Factors:
A natural number that divides a given integer perfectly is referred to as a factor.
Every number has itself and \( 1 \) as at least two factors.
e.g.
- Factors of \( 4 \) are \( 1,2 \) and \( 4 \)
- Factors of \( 8 \) are \( 1,2,4 \) and \( 8 \)
Prime Numbers:
A natural number with only two different factors is known as a prime number. (\( 1 \) and itself)
\( 2,3,4,5,7,11,13,19. . .\) are prime numbers.
- Keep in mind that \( 2 \) is the only even prime number.
Composite numbers:
A natural number with more than two factors is called a composite number.
\( 6,8,10,12,14,15,16. . . \) are composite numbers.
- \( 1 \) is neither prime nor composite as it has only one factor
Square numbers:
A number which is the result of multiplying a number by itself is known as a square number.
e.g.
- \( 4=2×2, 8=4×4, 9=3×3, 25=5×5 \)
So, \( 4, 8, 9 \) and \( 25 \)are square numbers.
- \( x \times x \) can be displayed as \( x^2\)
- First ten square numbers are \( 1,4,9,16,25,36,49,64,81,100 \).
Cube numbers:
A number which is the result of multiplying a number by itself twice is known as a
cube number.
e.g.
- \( 8=2×2×2 \), \( 27=3×3×3 \), \( 64=4×4×4 \)
So \( 8 \), \( 27 \) and \( 64 \) are cube numbers.
- \( x \times x\times x \) can be displayed as \( x^3 \)
- First \( 10 \)cube numbers are \( 1,8,27,64,125,216,343,512,729,1000 \).
Indices:
A handy approach to write a sequence of multiplications of the same number is to use an index (indices plural).
- They are frequently referred to as powers and exponents.
- For instance, \( 5×5×5×5 \)can be expressed as \( 5^4 \), which is the number \( 5 \) multiplied by itself four times
- \( x\times x\times x\times y \times z \times z \)can be expressed as \( x^3 \times y \times z^2 \) in index form.