- 4 Sections
- 132 Lessons
- 365 Days
- 1. Numbers32
- 1.11.1.1 Types of numbers
- 1.21.1.3 Mathematical Operations
- 1.31.1.4 Number Operations
- 1.41.1.5 Prime Factor Decomposition
- 1.51.2.1 Set Notation
- 1.61.2.2 Venn Diagrams
- 1.71.3.1 Powers/Indices and roots
- 1.81.3.2 Standard Form
- 1.91.3.3 Working with standard form
- 1.101.4.1 Fractions
- 1.111.4.2 Working with Fractions
- 1.121.4.3 Decimals
- 1.131.5.1 Percentage
- 1.141.5.2 Working with Percentage
- 1.151.6.1 Conversions
- 1.161.6.2 Ordering
- 1.171.7.1 Ratios
- 1.181.7.2 Working with Ratios
- 1.191.8.1 Proportion
- 1.201.9.1 Rounding
- 1.211.9.2 Estimation
- 1.221.9.3 Bounds
- 1.231.10.1 Using a Calculator
- 1.241.11.1 Time
- 1.251.11.2 Currency
- 1.261.11.3 Currency Conversion
- 1.271.12.1 Simple Interest
- 1.281.12.2 Compound interest
- 1.291.12.3 Depreciation
- 1.301.13.1 Exponential growth
- 1.311.13.2 Exponential decay
- 1.321.14.1 Compound measures
- 2. Algebra and Graphs39
- 2.12.1.1 Algebra Notation
- 2.22.1.2. Algebra Vocabulary
- 2.32.1.3. Algebra Basic
- 2.42.2.1 Algebraic roots & Indices
- 2.52.3.1 Expanding brackets
- 2.62.3.2 Factorisation
- 2.72.3.3 Quadratic expressions
- 2.82.3.4 Difference of two squares
- 2.92.4.1 Linear Equations
- 2.102.4.2 Linear Inequalities
- 2.112.5.1 Quadratic Equations
- 2.122.6.1 Rearranging formula
- 2.132.7.1 System of Linear Simultaneous Equations
- 2.142.7.2 System of quadratic simultaneous equations
- 2.152.8.1 Algebraic fractions
- 2.162.8.2 Working with algebraic fractions
- 2.172.8.3 Solving algebraic fractions
- 2.182.9.1 Forming equations
- 2.192.9.2 Equations & Problem solving
- 2.202.10.1 Introduction to functions
- 2.212.10.2 Composite & Inverse functions
- 2.222.11.1 Sequences
- 2.232.11.2 nth term
- 2.242.12.1 Midpoint of a line
- 2.252.12.2 Gradient of a line
- 2.262.12.3 Length of a line
- 2.272.13.1 Linear Graph
- 2.282.13.2 Quadratic Graphs
- 2.292.14.1 Types of Graphs
- 2.302.14.2 Drawing a graph without using a calculator
- 2.312.14.3 Drawing a graph with a calculator
- 2.322.14.4 Using a graph
- 2.332.14.5 Tangents
- 2.352.15.1 Drawing a Graph
- 2.362.15.2 Interpreting graphical inequalities
- 2.372.16.1 Distance-Time Graph
- 2.382.16.2 Speed-Time Graph
- 2.392.17.1 Differentiation
- 2.402.17.2 Applications
- 3. Geometry36
- 3.03.1.1 Symmetry
- 3.13.1.2 2D Shapes
- 3.23.1.3 3D shapes
- 3.33.1.4 Unit conversions
- 3.43.2.1 Basic angle Properties
- 3.53.2.2 Angle properties with triangle
- 3.63.2.3 Angle properties with quadrilateral
- 3.73.2.4 Angles in polygon
- 3.83.3.1 Bearings
- 3.93.3.2 Scale
- 3.103.3.3 Constructing SSS triangle
- 3.113.4.1 Angles at center & Semicircles
- 3.123.5.1 Perimeter
- 3.133.5.2 Area
- 3.143.5.3 Problems Solving with Areas
- 3.153.6.1 Arc
- 3.163.6.2 Sector
- 3.173.7.1 Volume
- 3.183.7.2 Surface area
- 3.193.8.1 Congruence
- 3.203.8.2 Similarity
- 3.213.9.1 Pythagoras Theorem
- 3.223.9.2 Right-angled Trigonometry
- 3.233.10.1 Sine Rule
- 3.243.10.2 Cosine Rule
- 3.253.10.3 Area of Triangle
- 3.263.10.4 Applications of Trigonometry
- 3.273.11.1 Pythagoras in 3D
- 3.283.12.1 Drawing trigonometric graph
- 3.293.12.2 Solving trigonometric equations
- 3.303.13.1 Basic Vectors
- 3.313.13.2 Vector problem solving
- 3.323.14.1 Translation
- 3.333.14.2 Rotation
- 3.343.14.3 Reflection
- 3.353.14.4 Scaling
- 4. Probability and Statistics25
- 4.04.1.1 Basic probability
- 4.14.1.2 Relative Frequency
- 4.24.1.3 Expected Frequency
- 4.34.2.1 Two way Tables
- 4.44.2.2 Probability & Venn Diagram
- 4.54.2.3 Tree Diagram
- 4.64.3.1 Conditional probability
- 4.74.3.2 Combined conditional probabilities
- 4.84.4.1 Mean, median & mode
- 4.94.4.2 Averages from Tables and Charts
- 4.104.4.3 Averages from Grouped Data
- 4.114.4.4 Comparing Distributions
- 4.124.5.1 Stem & Leaf diagrams
- 4.134.5.2 Bar chart
- 4.144.5.3 Pictogram
- 4.154.5.4 Pie chart
- 4.164.5.5 Frequency polygon
- 4.174.5.6 Working with Statistical Diagram
- 4.184.6.1 Frequency Density
- 4.194.6.2 Histograms
- 4.204.7.1 Cumulative frequency
- 4.214.7.2 Box-and-whisker Plots
- 4.224.8.1 Correlation
- 4.234.8.2 Scatter Graph
- 4.244.8.3 Line of best Fit
1.1.3 Mathematical Operations
There are four basic mathematical operations
Addition \( + \)
Subtraction \( – \)
Multiplication \( \times \)
Division \( \div \)
Other Useful Symbols
● Equal to \( = \)● Not equal to \( \neq \)
● Approximately equal to \( ≅ \)
● Almost equal to \( \approx \)
● Identical to \( \equiv \)
● Less than \( < \)
● Less than or equal to \( \leq \)
● Greater than \( > \)
● Greater than or equal to \( \geq \)
● Brackets \( () \)
● Square root \( \sqrt{} \)
● Plus, minus \( \pm \)
● Pi \( \pi \)<
Order of Operations (BODMAS/BIDMAS)
If there are many operations, they must be performed out in the order listed below:
Brackets
First, carry out any calculations included within any brackets.
Order/Index
Powers, roots, and reciprocals are among them.
Division
Multiplication
Addition
Subtraction
Worked Example:
Work out \( 5^3 \times (4+9) -10 \)First, carry out any calculations included within the brackets. \( 5^3 \times 13 – 10 \)
Then any power \( 125 \times 13 – 10 \)
Followed by multiplication \( 1625-10 \)
Now deal with subtraction \( 1615 \)
\( 5^3 \times (4+9) -10 = 1615 \)
Exam Tip
Recheck your answer by using calculator even if a question asks you to perform calculation without using calculatorTest your self
Insert one pair of brackets to make this calculation correct.
\( 5+3 \times 9 -2^2 =68 \)
[1]
Write down a cube number greater than \( 10 \) but less than \( 30 \).
[1]
Work out the difference between the two square numbers in the list below.
\( 25 \) \( 22 \) \( 17 \) \( 36 \) \( 39 \) \( 44 \) \( 5 \)
[2]
Negative Numbers:
Any numbers less than zero and have a negative or minus sign \( (−) \) in front of them are negative numbers.
Numbers greater than zero are referred to as positive numbers. If there is no sign in front of the number the number is positive.
Number Line:
Negative numbers are on the left side of zero whereas positive numbers are on the right.
Working with negative numbers:
- Adding/subtracting:
- Adding a negative number in a positive number is same as subtracting the positive number
e.g. \( 5+ (-3)=5-3=2 \)
- While adding two negative numbers, add absolute value of each number and put a negative sign in front, and you will get the answer
e.g. \( (-5)+ (-3)=-5-3=-8 \)
- Subtracting a negative number from a positive number is same as adding two positive numbers
e.g. \( 5- (-3)=5+3=8 \)
- While subtracting a negative number from another negative number you are actually adding a positive number into a negative number
e.g. \( -5- (-3)=-5+3=-2 \)
- Multiplication/Division
- Two numbers with the same sign changes into a positive number
e.g. \( (-10) \times (-2)=20 \) and \( 10 \times 2=20 \)
OR
\( (-10) \div (-2)=5 \) and \( 10 \div2=5 \)
- Two numbers with the different sign changes into a negative number
e.g. \( (-10) \times 2=-20 \) and \( 10 \times (-2)=-20 \)
OR
\( (-10) \div 2=-5 \) and \( 10 \div (-2)= -5 \)
Exam Tip
While working with negative numbers, on your calculator, you need to use brackets to ensure that it understands a number is negative.
Because \( (-3)^2 \neq -3^2 \)
You might find the following tables useful for remembering the rules for working with negative numbers.
Multiplication
Division
Worked Example:
Work out \( -18\div (-6)-2\times (-3)^2 \)
Starting with indices
\( -18 \div (-6)-2 \times 9 \)
Then division
\( 3-2 \times 9 \)
Followed by multiplication
\( 3-18 \)
And finally
\( -15 \)
\( -18 \div (-6)-2 \times (-3)^2=-15 \)
Tip:
For verification of answer, use your calculator.
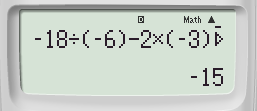
Test your self
Work out \( -2-10 \)
[1]
Work out \( -11- (-21) \)
[1]
<p>Work out \( 144 \div (-2) \)</p>
<p>[1]</p>
Work out \( 80 \div (-8) + (2 \times 9 ) -5^2 \)
[1]
At noon the temperature in Maseru was \( 21°C \).
At midnight the temperature had fallen by \( 26°C \).
Work out the temperature at midnight
[1]
