1.1.4 Number Operations
Addition:
To add two large numbers without calculator- Write greater number above the smaller in two rows
- Keep adding the digits one by one starting from one’s column
- If the sum is of two digits, write the value of ones below the line and value of tens at the top of the next column
- If the sum of the last column is a two-digit number, write it as it is below the line
Worked Example:
Find a total of \( 89563 \) and \( 3657 \) without using calculator.
Write the greater number above the smaller
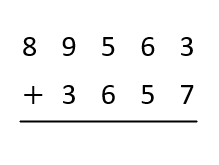
Add the digits in ones column, write \( 1 \) above to the next column
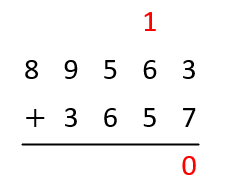
Add the digits in tens column including the \( 1 \)
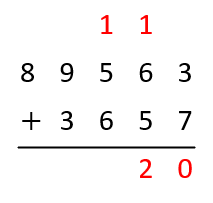
Continue to add in the same manner
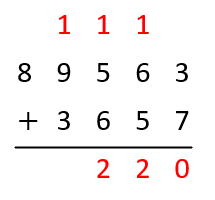
Subtraction:
To subtract a large number from another large number without calculator
Write greater number above the smaller in two rows
Calculate each column’s top number by deducting the column’s bottom number starting from one’s column
If subtraction produces a negative number, borrow a ten from the left column
Worked Example:
Work out the difference between 596 and 187 without using calculator.
Write the greater number above the smaller
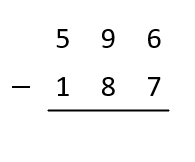
If we subtract \( 7 \) from \( 6 \) the answer will be \( -1 \),To avoid this we borrow \( 10 \) from \( 9 \)
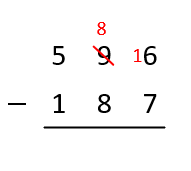
Now it will be \( 16-7=9 \)
Now in tens column it will be \( 8-8=0 \)
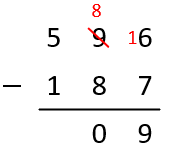
And finally in hundreds column it is \( 5-1=4 \)
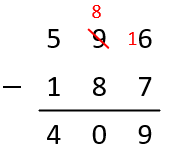
Tip:
Verify the answer by calculator
Addition/Subtraction with decimals:
While working with decimals
Make sure the decimal points are lined up in a column
Maintain the decimal point in the answer in this column as well.
Where required, enter 0s
Worked Example:
Find the sum of \( 0.96 \) and \( 59.3 \) without using calculator.
Write the greater number above the smaller keeping decimal in a column and fill the spaces with \( 0 \)
Add the digits in ones and tens column and write one above the left column and put the decimal in a column
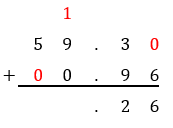
Continue in the same manner
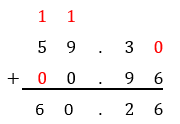
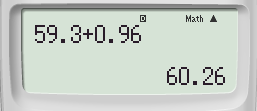
Tip:
Verify the answer by calculator
Multiplication:
Multiplication is simply a product of given numbers. And in general, it is represented by ‘\( × \)’ cross.
To multiply two integers without calculator
Multiply the ones digit of the bottom number by the whole top number
Place \( 0 \) at the ones place
Multiply the tens digit of the bottom number by the whole top number
When each bottom number is multiplied then add all the products together to have the final product
Worked Example:
Work out the product of \( 5963 \) and \( 24 \) without using calculator.
Write the greater number above the smaller
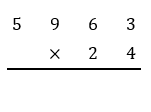
Multiply \( 4 \) by \( 5963 \) starting with \( 3 \).
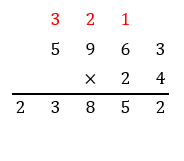
Now place \( 0 \) at one’s place and multiply \( 2 \) by \( 5963 \).
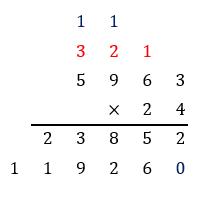
Now add the two products together to get the final product.
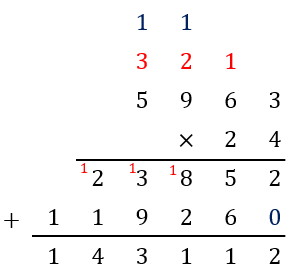
Tip:
Verify the answer by calculator
Division:
A division is a process of splitting a specific amount into equal parts. Division is opposite of multiplication. It is represented by \( \div \) or / between the numbers.
To perform long division, you must understand the following parts
Dividend
The number which has to be divided
Divisor
The number which divides the dividend
Quotient
The result of division
Remainder
The number left after the division which can’t be divided further
To perform long division
Take the dividend’s first digit starting on the left. The divisor must be smaller than or equal to this digit.
Following that, divide it by the divisor, and write the result as the quotient on top.
Subtract the result from the digit and write the difference below.
Bring the dividend’s next digit down.
Repeat the process
Worked Example:
Without using calculator, divide \( 435 \) by \( 4 \).
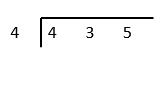
First digit of dividend is \( 4 \) which is equal to \( 4. 4\div 4=1 \)
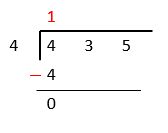
Now bring the second digit of dividend down and place it beside \( 0 \)
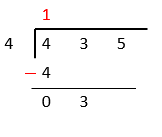
As \( 3<4 \), so we will put \( 0 \) in the quotient and bring the next digit down
Multiplication with decimals:
Multiply the decimals as if they were the whole numbers
Count the number of decimal places in each factor
The number of decimal places in the products is the sum of the number of decimal places in each factor
Worked Example:
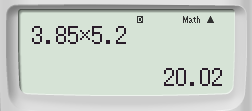
Without using calculator, Find the product of \( 3.85 \) and \( 5.2 \).
Multiply the decimals as they are whole numbers
Count the number of decimal places in each factor
As \( 2+1=3 \), So the number of decimal places in the product is \( 3 \)
Tip:
Verify the answer by calculator
