- 17 Sections
- 105 Lessons
- 365 Days
- 1. Measurement and Unitssome information5
- 2. Mass, Weight, & Density6
- 3. Motion5
- 4. Effect of Forces8
- 5 Moments & Momentum7
- 6. Energy, Work, Power & Pressure11
- 7. Kinetic Particle Model of Matter | Thermal physics5
- 8. Thermal Properties & Temperature | Thermal Physics5
- 9. Transfer of Thermal Energy | Thermal Physics5
- 10 Properties of Waves | Waves10
- 11. Light | Waves11
- 11.011.1 Reflection of Light
- 11.111.2 Investigating Reflection
- 11.211.3 Image Formation
- 11.311.4 Refraction of Light
- 11.411.5 Refractive Index | Snell’s Law
- 11.511.6 Total Internal Reflection
- 11.611.7 Thin Lenses & Ray Diagram
- 11.711.8 Diverging Lens
- 11.811.9 Short and Long Sightedness
- 11.911.10 Dispersion of Light
- 11.10Quiz – Light13 Questions
- 12. Electromagnetic Spectrum | Waves4
- 12. Electricity & Magnetism5
- 13. Electrical Quantities | Electricity11
- 14.013.1 Electrical Quantities
- 14.113.2 Electrical Conductors and Insulators
- 14.213.3 Electric Field
- 14.313.4 Electric Current
- 14.413.5 Direct Current and Alternating Current
- 14.513.6 Electromotive Force and Potential Difference
- 14.613.7 Resistance
- 14.713.8 Current Voltage Graphs
- 14.813.9 Electrical Resistance
- 14.913.10 Electrical Energy and Electrical Power
- 14.10Quiz 13 – Electrical Quantities21 Questions
- 14. Electrical Circuits7
- 15. Electromagnetic Effects14
- 16.015.1 – Electromagnetic Induction
- 16.115.2 Len’z Law
- 16.215.3 Electromagnetic Effects4 Questions
- 16.315.4 The A.C Generator
- 16.415.5 Quiz – The A.C Generator2 Questions
- 16.515.6 The D.C Motor
- 16.615.7 The D.C Motor3 Questions
- 16.715.8 Magnetic Effect of a Current
- 16.815.9 Magnetic Field Patterns Experiment
- 16.915.10 Magnetic Effect of a Current3 Questions
- 16.1015.11 Force on a current-carrying conductor
- 16.1115.12 Force on a current-carrying conductor2 Questions
- 16.1215.13 – The transformer
- 16.1315.14 – The transformer6 Questions
- 5. Nuclear Physics10
5.2 Moments
Chapter 1 | Motion, Forces and Energy
5.2- Principle of moments
According to the principle of moments, an object is in balance only when the total anticlockwise moment equals the total clockwise moment about the pivot.
Key Points:
Moment of Force:
- The moment of a force is its turning effect, calculated by multiplying the force by the perpendicular distance from the pivot point.
Pivot or Fulcrum:
- The pivot is the fixed point around which the object can rotate.
- Forces applied at different distances from the pivot create different moments.
Equilibrium Conditions:
- For an object to be in equilibrium:
- Total anticlockwise moment = Total clockwise moment.
- For an object to be in equilibrium:
Mathematical Representation:
- Mathematically, this principle is expressed as Clockwise Moment = Anticlockwise Moment
Application:
- The Principle of Moments is commonly used in solving problems involving levers, see-saws, and any situation where objects are balanced or in rotational equilibrium.
Balancing Equations:
- When solving problems, the moments are balanced by ensuring that the product of force and distance on one side of the pivot is equal to the product on the other side.
Clockwise Moment
The balancing equation can then be written as:
Unit:
- The unit of moment is the newton-meter (Nm).
Example:
Mark and Alex are at opposite ends of a teeter-totter. The Mark weighs 700 N and the Alex weighs 150 N. Mark sits 0.4 m from the pivot. Calculate the distance Alex must sit from the pivot for the teeter-totter to be balanced.
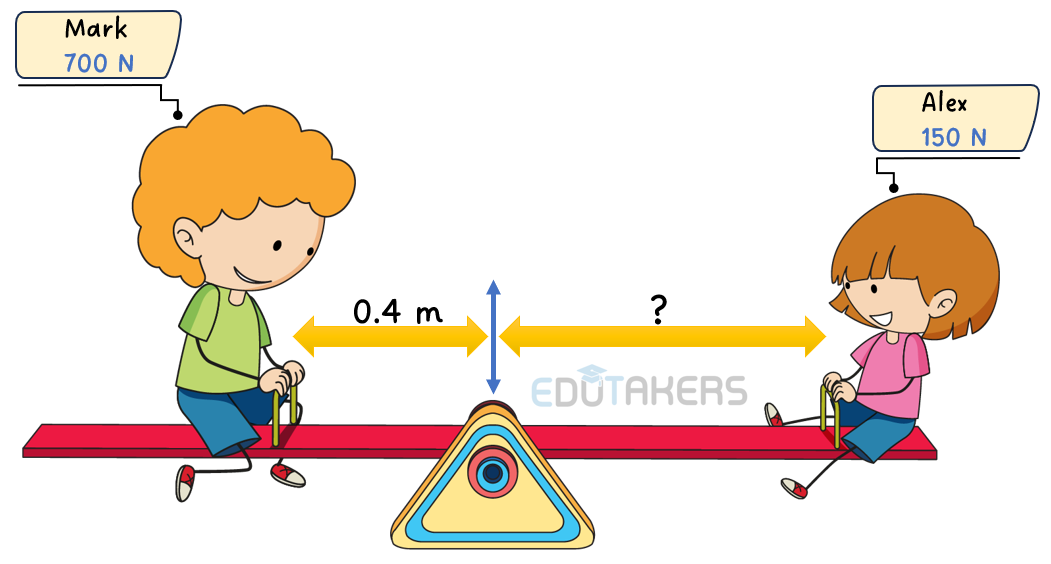
Given Information:
- Weight of Mark () = 700 N
- Weight of Alex () = 150 N
- Distance of Mark from pivot () = 0.4 m
- Distance of Alex from pivot () = ?
The teeter-totter is in equilibrium, so the
Clockwise moment = Anticlockwise moment
Calculation:
Using the principle of moments
Mathematically, .
Step 1: Set Up the Equation
Step 2: Solve for
Step 3: Perform the Calculation
Therefore, Alex must sit approximately 1.87 meters away from the pivot for the see-saw to be balanced.
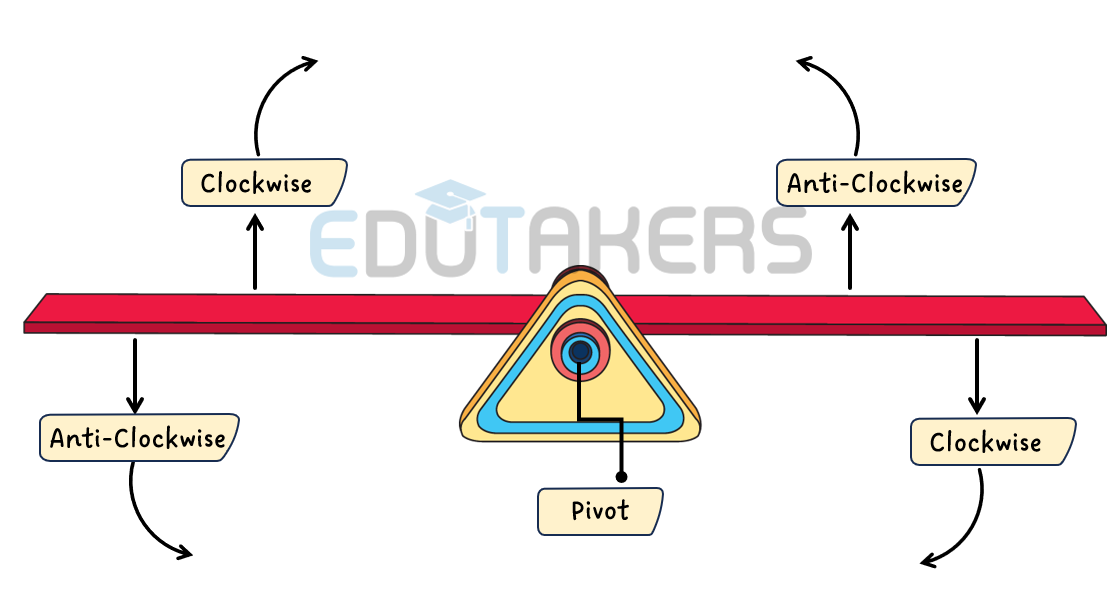
More than one Force
Figure: Diagram showing the moments due to large number of forces acting on balanced beam.
Generalization:
If more than one force is acting on each side of the pivot, the principle of moments extends to the total clockwise moment equaling the total anticlockwise moment.
(Clockwise moment = anticlockwise moment).
Clockwise moment = Anticlockwise moment
- Clockwise moment = Anticlockwise moment signifies equilibrium in a rotational system.
- The total turning effect due to clockwise forces equals the total turning effect due to anticlockwise forces.
- Applied to scenarios like seesaws, it ensures balance between forces and distances around a pivot
❓ Exam Question
0625/0972/21-Oct-Nov-2020-Q7
A uniform plank rests on a pivot at its centre.
Two children P and Q sit on the plank in the positions shown.
The mass of child P is 25 kg.
The plank is balanced.
What is the mass of child Q?
0625/0972/22-Feb-Mar-2020-Q9
An athlete with mass 70 kg trains by performing press-ups with a load on his back. The diagramshows the perpendicular distances involved.
The centre of mass of the athlete is CM and the centre of mass of the load he is carrying is CL
The mass of the load is 6.0 kg.
What is the upward force exerted by his two arms?
5.2- Principle of moments
According to the principle of moments, an object is in balance only when the total anticlockwise moment equals the total clockwise moment about the pivot.
Key Points:
Moment of Force:
- The moment of a force is its turning effect, calculated by multiplying the force by the perpendicular distance from the pivot point.
Pivot or Fulcrum:
- The pivot is the fixed point around which the object can rotate.
- Forces applied at different distances from the pivot create different moments.
Equilibrium Conditions:
- For an object to be in equilibrium:
- Total anticlockwise moment = Total clockwise moment.
- For an object to be in equilibrium:
Mathematical Representation:
- Mathematically, this principle is expressed as Clockwise Moment = Anticlockwise Moment
Application:
- The Principle of Moments is commonly used in solving problems involving levers, see-saws, and any situation where objects are balanced or in rotational equilibrium.
Balancing Equations:
- When solving problems, the moments are balanced by ensuring that the product of force and distance on one side of the pivot is equal to the product on the other side.
Clockwise Moment
The balancing equation can then be written as:
Unit:
- The unit of moment is the newton-meter (Nm).
Example:
Mark and Alex are at opposite ends of a teeter-totter. The Mark weighs 700 N and the Alex weighs 150 N. Mark sits 0.4 m from the pivot. Calculate the distance Alex must sit from the pivot for the teeter-totter to be balanced.

Given Information:
- Weight of Mark () = 700 N
- Weight of Alex () = 150 N
- Distance of Mark from pivot () = 0.4 m
- Distance of Alex from pivot () = ?
The teeter-totter is in equilibrium, so the
Clockwise moment = Anticlockwise moment
Calculation:
Using the principle of moments
Mathematically, .
Step 1: Set Up the Equation
Step 2: Solve for
Step 3: Perform the Calculation
Therefore, Alex must sit approximately 1.87 meters away from the pivot for the see-saw to be balanced.
More than one Force
Figure: Diagram showing the moments due to large number of forces acting on balanced beam.
Generalization:
If more than one force is acting on each side of the pivot, the principle of moments extends to the total clockwise moment equaling the total anticlockwise moment.
(Clockwise moment = anticlockwise moment).
Clockwise moment = Anticlockwise moment
- Clockwise moment = Anticlockwise moment signifies equilibrium in a rotational system.
- The total turning effect due to clockwise forces equals the total turning effect due to anticlockwise forces.
- Applied to scenarios like seesaws, it ensures balance between forces and distances around a pivot

❓ Exam Question
0625/0972/21-Oct-Nov-2020-Q7
A uniform plank rests on a pivot at its centre.
Two children P and Q sit on the plank in the positions shown.
The mass of child P is 25 kg.
The plank is balanced.
What is the mass of child Q?
0625/0972/22-Feb-Mar-2020-Q9
An athlete with mass 70 kg trains by performing press-ups with a load on his back. The diagramshows the perpendicular distances involved.
The centre of mass of the athlete is CM and the centre of mass of the load he is carrying is CL
The mass of the load is 6.0 kg.
What is the upward force exerted by his two arms?
